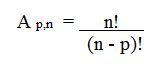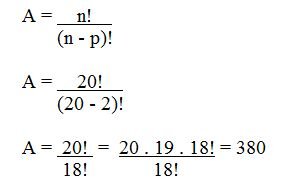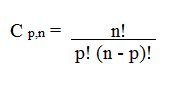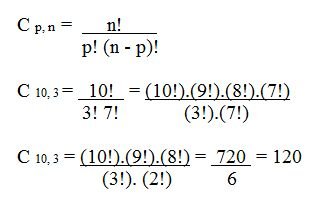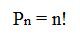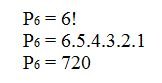Equações do primeiro grau

Equações do primeiro grau são expressões algébricas que envolvem uma igualdade. Por serem expressões algébricas, as equações envolvem números e letras. Essas letras representam números até então desconhecidos e são chamadas de incógnitas.

• Primeiro e segundo membros da equação de 1º grau

Tendo como ponto de partida o sinal de igualdade, uma equação do primeiro grau possui dois membros. O primeiro membro é composto por todos os números e letras presentes à esquerda do sinal de igual. O segundo membro é composto por todos os números e incógnitas presentes à direita da igualdade. Dessa maneira, tomando a equação 4x + 16 = 2x – 8 como exemplo, 4x + 16 é o primeiro membro e 2x – 8 é o segundo membro.

• Termo da equação de 1º grau

Cada elemento pertencente a um membro da equação do primeiro grau é chamado de termo. Assim sendo, com base no exemplo anterior, 4x, 16, 2x e -8 são os termos presentes no primeiro e segundo membros da equação.

• Grau da equação de 1º grau

O grau de uma equação é dado por um dos termos que possui incógnita. Para isso, observe entre as incógnitas aquela que possui maior expoente. Nas equações do primeiro grau, os expoentes das incógnitas são sempre 1 e, por isso, não aparecem. Equações de segundo grau têm pelo menos uma incógnita elevada ao quadrado; as do terceiro grau possuem pelo menos uma incógnita elevada ao cubo e assim por diante.

• Como resolver uma equação do primeiro grau?

Resolver uma equação é encontrar o valor numérico de x que faz com que a igualdade da equação seja verdadeira. A estratégia para encontrar o valor de x é isolá-lo no primeiro membro. Por exemplo, observe a equação:

2x = 6

Para resolvê-la, é necessário encontrar um valor que, multiplicado por 2, tenha 6 como resultado. Esse valor é 3, pois 2·3 = 6. Desse modo, a solução da equação deve ser escrita da seguinte maneira:

2x = 6

x = 3

Observe que, em x = 3, isolamos x no primeiro membro e escrevemos seu resultado no segundo. Descobrir o resultado de equações que envolvem apenas a tabuada, como a anterior, é tarefa fácil e pode ser feito por meio de tentativa e erro. Porém, não é preciso dificultar muito a equação para que esse método (tentativa e erro) falhe ou exija muitas tentativas. Observe, por exemplo, a equação:

5x = 25
3        

Para resolver essa equação, procuramos um número que, multiplicado por 5 e dividido por 3, tenha 25 como resultado. Note que o resultado dessa equação não é tão óbvio quanto o resultado da última. É possível testar as possibilidades de resultado até encontrar o resultado correto, contudo, o melhor caminho para encontrá-lo seria o uso da propriedade fundamental das equações.

• Propriedade fundamental das equações

A propriedade fundamental das equações é utilizada como um dos métodos de resolução de equações. Esse método é pouco utilizado no Brasil, mas possui a grande vantagem de se resumir a uma única regra. A propriedade fundamental das equações é a seguinte:

Qualquer operação feita no primeiro membro de uma equação, desde que também seja feita igualmente no segundo membro, não modifica os seus resultados.

Essa propriedade é conhecida como regra da balança, pois o que é feito no primeiro membro da equação deve ser repetido no segundo. Observe:

1 – Qual é o valor de x na equação 2x = 6?

Para resolver essa equação seguindo a regra da balança, divida os dois membros por 2. Note que, dessa maneira, no primeiro membro, restará apenas x, pois 2 dividido por 2 é 1 e 1 vezes x é x. Já no segundo membro, teremos o resultado 3. Observe:

2x = 6

2x = 6
2     2

1x = 3

x = 3

2 – Qual é o valor de x na equação x + 7 = 14?

Dessa vez, para isolar x no primeiro membro, devemos utilizar a subtração. Basta subtrair 7 dos dois membros da equação para encontrar o seu resultado. Observe:

x + 7 = 14

x + 7 – 7 = 14 – 7

x = 7

3 – Qual é o valor numérico de x na equação 2x + 7 = 17

Pode-se dividir o trabalho em dois passos. Primeiramente faça subtrações e adições para isolar o termo que possui x do lado esquerdo. Depois, faça multiplicações e divisões para isolar x no primeiro membro. Observe:

2x + 7 = 17

2x + 7 – 7 = 17 – 7

2x = 10

2x = 10
2      2

1x = 5

x = 5

4 – Qual é o valor numérico da equação: 4x + 7 = 2x – 7?

Antes de mais nada, é preciso que os termos que possuem incógnita estejam todos no primeiro membro. Portanto, subtrairemos 2x em ambos os membros para que 2x seja eliminado no segundo. Observe:

4x + 7 – 2x = 2x – 7 – 2x
4x + 7 – 2x = – 7

Agora, é necessário deixar no primeiro membro apenas termos que possuem incógnita. Portanto, para que 7 seja eliminado do primeiro membro, subtrairemos 7 em ambos os membros dessa equação.

4x + 7 – 2x – 7 = – 7 – 7

4x – 2x = – 14

2x = 14

Para finalizar, dividimos ambos os membros por 2 para que x fique isolado no primeiro membro.

2x = 14
2      2

1x = 7

x = 7

Análise Combinatória

Exercícios Princípio fundamental da contagem com resposta

1)  Thiago possui 3 blusas diferentes e 2 calças diferentes. De quantas maneiras ele poderá escolher uma blusa e uma calça para se vestir? Resposta:  6

2)  Quantos números de dois algarismos podem ser formados utilizando elementos do conjunto  {1, 2, 3}? Resposta:  9

3) Quantos números de dois algarismos diferentes (distintos) podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta:  6

4) Quantos números de três algarismos podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta:  27

5) Quantos números de três algarismos diferentes (distintos) podem ser formados utilizando elementos do conjunto {1, 2, 3}? Resposta:  6

6)  Um estádio possui 4 portões. De quantas maneiras diferentes um torcedor pode entrar e sair desse estádio? Resposta:  16

7)  Um estádio possui 4 portões. De quantas maneiras diferentes um torcedor pode entrar e sair desse estádio utilizando, para sair, um portão diferente do que entrou? Resposta:  12

8)  Mariana desenhou uma bandeira retangular de 3 listras e deseja pintá-la, de modo que duas listras consecutivas não sejam pintadas da mesma cor. Se ela possui 4 lápis de cores diferentes, de quantas maneiras poderá pintar sua bandeira? Resposta:  36

9)  Numa prova havia 4 itens para que os alunos respondessem V (verdadeiro) ou F (falso). De quantas maneiras diferentes um aluno que vai “chutar” todas as repostas poderá responder esses itens? Resposta:  16

10)  Um painel luminoso retangular é composto por 5 lâmpadas. De quantas maneiras diferentes esse painel pode estar iluminado? (considera-se o painel iluminado se, pelo menos, uma de suas lâmpadas estiver acesa) Resposta:  31

11)  Quantos numeros de 3 algarismo distintos podem ser formados usando-se os algariasmo 1,2,3,4 e 5?

12)   Um restaurante ofereçe no cardapio 2 saladas distintas,e 4 tipodes de pratos de carne,5 variedades de bebidas e 3 sobremesas diferentes. Uma pessoa deseja uma salada,um prato de carne,uma bebida e uma sobremesa.De quantas maneiras a pessoa podera fazer seu pedido?

13)  Quatro times de futebol(Vasco,Atletico,Corinthians e Internacional ) disputam um torneio.Quantos e quais são as possibilidades de classificação para os três primeiros lugares?

14)   Numa eleição de uma escolahá 3 candidatos a presidente,cinco a vice-presidente,¨a secretario e 7 a tesoreiro.Quantos podem ser os resultados da eleição?

 EXERCÍCIOS COMPLEMENTARES

15) Com os algarismos 1, 2, 3, 4, 5 e 6, quantos números de três algarismos distintos podemos formar?

a) 30      b) 60      c) 90      d) 120      e) 150

16) Uma prova consta de 10 questões do tipo V ou F. De quantas maneiras distintas ela pode ser resolvida?

a) 128      b) 256      c) 512      d) 1024      e) 2048

17) Quantos números de três algarismos podemos com os algarismos 0, 1, 2, 3, 4, 5, 6 e 7?

a) 348      b) 448      c) 548      d) 648      e) 748

18) Quantos números ímpares de três algarismos distintos podemos formar com os algarismos 0, 1, 2, 3, 4, 5, 6 e 7?

a) 72      b) 144      c) 200      d) 240      e) 288

19) Um jantar constará de três partes: entrada, prato principal e sobremesa. De quantas maneiras distintas ele poderá ser composto, se há como opções oito entradas, cinco pratos principais e quatro sobremesa?

a) 160      b) 150      c) 120      d) 80      e) 17 

20) Se um quarto tem 5 portas, o número de maneiras distintas de se entrar nele e sair dele por um porta diferente é:

a) 5      b) 10      c) 15      d) 20      e) 25 

21) Quantos números de 4 algarismos diferentes têm o algarismo da unidade de milhar igual a 3?

a) 1512      b) 1008      c) 504      d) 3024      e) 2520

22) Cinco sinaleiros estão alinhados. Cada um tem três bandeiras: uma amarela, uma verde e uma vermelha. Os cinco sinaleiros levantam uma bandeira cada, ao mesmo tempo, transmitindo-se assim um sinal. A quantidade  de sinais diferentes que se pode transmitir é:

a) 15      b) 125     c) 243      d) 1215      e) 729 

23) Com os algarismos 1, 2, 3, 4, 5 e 6 são formados números de quatro algarismos distintos. Dentre eles são divisíveis por 5:

a) 20 números      b) 30 números      c) 60 números      d) 120 números      e) 180 números 

24) Uma estrada de ferro tem 10 estações. Quantos tipos distintos de bilhetes existem em circulação, sabendo-se que cada bilhete contém impressos apenas a estação de partida e a estação de chegada? (Supondo que o trem tem vagões de apenas uma classe)

a) 28      b) 45      c) 20      d) 56      e) 90

GABARITO COMPLEMENTARES

15- D

16- D

17- B

18- B

19- A

20- D

21- C

22- C

23- C

24- B 




http://www.matematiques.com.br

terça-feira, 9 de maio de 2017

Análise combinatória: arranjos, combinações, permutações e princípio multiplicativo em teoria e exercícios com gabarito

Princípio Fundamental da Contagem

O princípio fundamental da contagem postula que:

“quando um evento é composto por n etapas sucessivas e independentes, de tal modo que as possibilidades da primeira etapa é x e as possibilidades da segunda etapa é y, resulta no número total de possibilidades de o evento ocorrer, dado pelo produto (x) . (y)”.

Em resumo, no princípio fundamental da contagem, multiplica-se o número de opções entre as escolhas que lhe são apresentadas.

Como exemplo, podemos pensar na combinação de roupas de uma garota, sendo que ela possui 3 tipos de calças, 4 tipos de blusas, 2 tipos de sapatos e 3 tipos de bolsas.

Logo, para saber quais as diferentes possibilidades que a garota possui, formadas por suas peças de roupas, basta multiplicar o número de peças: 3 x 4 x 2 x 3 = 72.

Portanto, a garota possui 72 possibilidades de configurações diferentes para o uso das peças de roupas e dos acessórios apresentados.

Tipos de Combinatória

A combinatória utiliza de importantes ferramentas, ou seja, há três tipos básicos de agrupamento dos elementos: arranjos, combinações e permutações. Todas utilizam o fatorial:

Arranjos

Nos arranjos, os agrupamentos dos elementos dependem da ordem e da natureza dos mesmos.

Assim, para obter o arranjo simples de n elementos tomados p a p (p ≤ n), ou seja, para calcular os diferentes arranjos ordenados de tais elementos, utiliza-se a seguinte expressão:

Como exemplo de arranjo, podemos pensar nas eleições, de modo que 20 deputados concorrem a 2 vagas no estado de São Paulo.

Dessa forma, de quantas maneiras distintas a escolha poderá ser feita? Observe que nesse caso, a ordem é importante, visto que altera o resultado final.

Logo, o arranjo pode ser feito de 380 maneiras diferentes.

Combinações

As combinações são subconjuntos em que a ordem dos elementos não é importante, entretanto, são caracterizadas pela natureza dos mesmos.

Assim, para calcular uma combinação simples de n elementos tomados p a p (p ≤ n), utiliza-se a seguinte expressão:

A fim de exemplificar, podemos pensar na escolha de 3 membros para formar a comissão organizadora de um evento, dentre as 10 pessoas que se candidataram.

Para tanto, Maria, João e José são os escolhidos, porém de quantas maneiras distintas esse grupo pode se combinar? Note que, ao contrário dos arranjos, nas combinações, a ordem dos elementos não é relevante, ou seja, a combinação Maria, João e José é equivalente à João, José e Maria.

Logo, há 120 maneiras distintas de combinar os 3 membros da comissão.

Permutações

As permutações são agrupamentos ordenados, donde o número de elementos (n) do agrupamento é igual ao número de elementos disponíveis, expresso pela fórmula:

Para exemplificar, pensemos de quantas maneiras diferentes poderiam surgir a sequência de resultados dos 5 números que saíram na loteria: 11, 12, 44, 52, 61. Sendo assim, os números que compõem o resultado final é uma sequência de 6 números, logo:

Logo, o resultado final da loteria, podem ser permutados 720 vezes.

Exercícios de permutações simples

1.    De quantos modos distintos 5 pessoas podem sentar-se em um banco de jardim com 5 lugares?

Auxílio: P(n)=n!, n=5

Resposta: N=1×2×3×4×5=120

2.    De quantos modos distintos podemos colocar 3 livros juntos em uma estante de biblioteca?

Auxílio: P(n)=n!, n=3

Resposta: N=1×2×3=6

3.     De quantos modos distintos 5 pessoas podem sentar-se em um banco de jardim com 5 lugares?

Auxílio: P(n)=n!, n=5

Resposta: N=1×2×3×4×5=120

2.    Qual é o número possível de anagramas que se pode montar com as letras da palavra AMOR?

Auxílio: P(n)=n!, n=4

Resposta: N=1×2×3×4=24

3.  Quantos números com cinco algarismos podemos construir com os números ímpares 1,3,5,7,9.

Auxílio:

Resposta: P(5)=120.

4.   Quantos números com cinco algarismos podemos construir com os números ímpares 1,3,5,7,9, desde que estejam sempre juntos os algarismos 1 e 3.

Auxílio: Cada conjunto com os algarismos 13 e 31 forma um grupo que junto com os outros, fornece 4 grupos.

Resposta: N=2×P(4)=2×24=48

5.    Consideremos um conjunto com n letras. Quantas permutações começam por uma determinada letra?

Resposta: N=P(n-1)=(n-1)!

6.     Quantos são os anagramas possíveis com as letras: ABCDEFGHI?

Resposta: P(9)=9!

7.     Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando por A?

Resposta: P(8)=8!

8.     Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando por AB?

Resposta: P(7)=7!

9.     Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando por ABC?

Resposta: P(6)=6!

10.  Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando por uma das letras A, B ou C?

Auxílio: Começando por uma das letras A,B,C: P(8)=8!

Resposta: N=3×P(8)=3×8!

11.  Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando pelas três letras do grupo ABC?

Auxílio: Começando pelas letras do grupo ABC: P(3)=3!=6

Resposta: N=P(3)×P(6)=6×120=720

12.  Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando por uma vogal e terminando por uma consoante?

Auxílio: 3 são as vogais e 6 são as consoantes.

Resposta: N=P(3)×P(6)=6×120=720 (???)

13.  Há 10 pessoas em um local, sendo 3 com camisas verdes, 3 com camisas amarelas, 2 com camisas azuis e 2 com camisas brancas. De quantos modos podemos perfilar todas essas 10 pessoas de modo que os grupos com as camisas de mesma cor fiquem juntos?

Auxílio: Temos 4 grupos de camisas, logo P(4) posições para as equipes e os grupos podem permutar as suas posições, respectivamente, P(3), P(3), P(2) e P(2).

Resposta: N=P(4)×P(3)×P(3)×P(2)×P(2)=3456

Exercícios de permutações com repetição

16.  Quantos são os anagramas possíveis com as letras da palavra: ARARA?

Auxílio: A letra A aparece 3 vezes e a letra R aparece 2 vezes.

Resposta: Pr(5;3+2)=5!/(3!2!)=10

17.  Quantos são os anagramas possíveis para a palavra: ULYSSES?

18.  Quantos são os anagramas possíveis para a palavra: ULYSSES começando por U?

19.  Quantos são os anagramas possíveis para a palavra: ULYSSES terminando por S?

20.  Quantos são os anagramas possíveis para a palavra: ULYSSES começando por U e terminando por S?

21.  Qual é o número possível de anagramas que se pode montar com as letras da palavra AMA?

Auxílio: p1=n(A)=2, p2=n(M)=1, N=Pr(3;2+1)

Pr(p;p1+p2)=(p1+p2)!/(p1!p2!)

Resposta:N=3!/(2!1!)=3

22.  Qual é o número possível de anagramas que se pode montar com as letras da palavra AMAR?

Auxílio: N=(p1+p2+p3)!/(p1!p2!p3!),A=2,M=1,R=1

Resposta: N=4!/(2!1!1!)=12

23.  Qual é o número possível de anagramas que se pode montar com as letras da palavra ARARUNA?

Auxílio: N=(p1+p2+p3+p4)!/(p1!p2!p3!p4!), A=3, R=2, N=1, U=1

Resposta: N=7!/(3!2!1!1!)=420

24.  O número Pi com 10 algarismos (sem considerar a vírgula) é indicado por 3141592653. Quantas são as permutações diferentes que podemos construir com estes 10 algarismos

Auxílio: n(1)=n(3)=n(5)=2, n(2)=n(4)=n(6)=n(9)=1

Resposta: Pr(10,2+1+2+1+2+1+1)=10!/8=453600

25.  Quantos são os anagramas possíveis com as letras da palavra: MATEMATICA?

Auxílio: A letra A aparece 3 vezes, a letra M aparece 2 vezes, a letra T aparece 2 vezes, a letras E aparece 1 vez , a letra I aparece 1 vez e a letra C aparece 1 vez.

Resposta: Pr(10;3+2+2+1+1+1) = 10!/[3!2!2!1!1!1!] =151200

Exercícios de permutações circulares

26.  De quantos modos distintos 5 pessoas podem sentar-se em volta de uma mesa circular?

Auxílio: N=P(n-1)=(n-1)!, n=5

Resposta: N=1×2×3×4=24

27.  De quantos modos distintos 5 pessoas podem sentar-se em volta de uma mesa retangular?

Auxílio: N=P(n-1)=(n-1)!, n=5

Resposta: N=1×2×3×4=24

Exercícios de combinações simples

28.  Um indivíduo possui 25 livros diferentes. De quantas formas distintas ele poderá empacotar tais livros em grupos de 6 livros?

29.  Quantos grupos de 3 pessoas podem ser montados com 8 pessoas?

Auxílio: C=C(m,p)=m!/[p!(m-p)!]; m=8,p=3

Resposta: C=8!/(3!5!)=(8×7×6)/(1×2×3)=56

30.  Quantos grupos de 2 pessoas podem ser montados com 1000 pessoas?

Auxílio: C=C(m,p)=m!/[p!(m-p)!], m=1000, p=2

Resposta: C=1000!/(2!998!)=1000×999=999000

31.  Quantas combinações com 4 elementos podem ser montadas com as 10 primeiras letras do alfabeto?

Conceito: Combinação

Auxílio: C=C(m,p)=m!/[p!(m-p)!], m=10, p=4

Resposta: C=10!/(4!6!)=(10×9×8×7)/(1×2×3×4)=210]

32.  Quantas combinações com 4 elementos podem ser montadas com as 10 primeiras letras do alfabeto, de tal forma que sempre comecem pela letra A?

Auxílio: C=C(m1,p1).C(m-m1,p-p1), m=10, p=4, m1=1, p1=1

Resposta: C=C(1,1).C(9,3)=(1×9×8×7)/6=84

33.  Quantas combinações com 4 elementos podem ser montadas com as 10 primeiras letras do alfabeto, de tal forma que sempre estejam juntas as letras A e B?

Auxílio: C=C(m1,p1).C(m-m1,p-p1), m=10, p=4, m1=2, p1=2

Resposta: C=C(2,2).C(8,2)=(1×8×7)/2=28

34.  Quantas combinações com 4 elementos podem ser montadas com as 10 primeiras letras do alfabeto, de tal forma que não contenham nem as letras A e B?

Auxílio: C=C(m1,p1).C(m-m1,p-p1), m=10, p=4, m1=2, p1=0

Resposta: C=C(2,0).C(8,4)=(1×8×7×6×5)/24=70

35.  Quantas combinações com 4 elementos podem ser montadas com as 10 primeiras letras do alfabeto, de tal forma que somente uma das letras A ou B esteja presente, mas não as duas?

Auxílio: C=C(m1,p1).C(m-m1,p-p1), m=10, p=4, m1=2, p1=1

Resposta: C=C(2,1).C(8,3)=(2×8×7×6)/6=112

36.  Quantas combinações com 4 elementos podem ser montadas com as 10 primeiras letras do alfabeto, de tal forma que contêm 2 dentre as 3 letras A,B e C?

Auxílio: C=C(m1,p1).C(m-m1,p-p1), m=10, p=4, m1=3, p1=2

Resposta: C=C(3,2).C(7,2)=(3×7×6)/2=63

37.  Em uma sala existem 40 pessoas, 18 mulheres e 22 homens. Quantas comissões podem ser montadas nesta sala contendo 3 mulheres e 5 homens?

38.  Calcular o valor de m tal que 5 C(m+1,3)=2 C(m+2,2).

39.  Quantos triângulos podem ser traçados contendo pontos de duas retas paralelas, sabendo-se que em uma reta existem 6 pontos e na outra reta existem 5 pontos?

40.  Quantos quadriláteros convexos podem ser traçados contendo pontos de duas retas paralelas, sabendo-se que em uma reta existem 6 pontos e na outra reta existem 5 pontos?

41.  Em uma classe com 16 pessoas, há 10 homens e 6 mulheres. Consideremos H um certo homem e M uma certa mulher. Quantos grupos podemos formar:

a.     com 4 homens e 2 mulheres?

b.    contendo H mas não M?

c.     contendo M mas não H?

d.    contendo H e M?

e.     contendo somente H ou somente M?

42.  Quantos números diferentes maiores do que 100 e menores do que 1000 podem ser construídos com os algarismos 1,2,3,4,5 e 6, sendo:

a.     que cada algarismo aparece somente uma vez?

b.    que cada algarismo pode repetir até 3 vezes?

c.     os números pares sem repetição?

d.    os números ímpares sem repetição?

e.     os números pares com repetição?

f.     os números ímpares com repetição?

43.  Para resolver um assunto entre 6 professores e 4 alunos, devemos formar comissões com 3 professores e 2 alunos. Quantas são as possibilidades?

Resposta: N=C(6,3)×C(4,2)=30×6=180

44.  Desejamos formar comissões de 6 pessoas entre cinco pais de alunos e quatro professores. Quantas comissões terão somente 1 professor?

45.  Desejamos formar comissões de 6 pessoas entre cinco pais de alunos e quatro professores. Quantas comissões terão somente 2 professores?

46.  Desejamos formar comissões de 6 pessoas entre cinco pais de alunos e quatro professores. Quantas comissões terão no mínimo 2 professores?

47.  Desejamos formar comissões de 6 pessoas entre cinco pais de alunos e quatro professores. Quantas comissões terão no mínimo 3 professores?

48.  Num plano existem 4 pontos, sendo que 3 deles são não colineares. Qual é o número possível de retas que passam por esses pontos?

Resposta: C(4,2)=6

49.  Num plano colocamos n pontos, sendo que 3 deles são não colineares. Qual é o número possível de retas que passam por esses pontos?

Resposta: C(n,2)=n(n-1)/2

50.  Quatro pontos são postos num plano, sendo que 3 deles são não colineares. Qual é o número possível de triângulos construídos com esses pontos?

Auxílio: C(3,2)=3 triângulos para cada ponto.

51.  Qual é o número de diagonais de um polígono regular de n lados?

Resposta: N=C(n,2)-n=n(n-1)/2-n=n(n-3)/2

52. Qual é o número de diagonais de um cubo?

53.  Qual é o número de diagonais de um prisma regular cuja base tem 5 lados?

54.  Qual é o número de diagonais de um prisma regular cuja base tem 6 lados?

55.  Qual é o número de diagonais de um prisma regular cuja base tem n lados?

56.  Com as 5 vogais: A,E,I,O,U, construir o conjunto que contém todas as combinações tomadas 2 a 2.

57.  Com as letras: A,B,C,D,E,F,G e H, determinar o número das permutações possíveis que começam por ABC.

Resposta: N=P(5)=120.

58. Quantas digonais possui um dodecágono?

Resposta: N=12×9/2=54

59.  Quantas digonais possui o tetraedro regular?

Resposta: N=0

60.  Quantas digonais possui um prisma triangular regular?

Resposta: N=0

Exercícios de combinações com repetição

61.  Determinar o número de combinações com 4 elementos tomados com repetição de 7 livros.

Auxílio: Cr=Cr(m,p)=C(m+p-1,p), m=7, p=4

Resposta: Cr=Cr(7,4)=C(7+4-1,4)=C(10,4)=210

62.  Determinar o número de combinações com repetição de 4 objetos tomados 2 a 2.

Auxílio: Cr=Cr(m,p)=C(m+p-1,p), m=4, p=2

Resposta: Cr=Cr(4,2)=C(4+2-1,2)=C(5,2)=10

Exercícios de arranjos simples

63.  Quantos números diferentes com 1 algarismo, podemos formar com os algarismos: 0,1,2,3,4,5,6,7,8 e 9.

Resposta: N1=A(9,1)=9

64.  Quantos números distintos com 2 algarismos diferentes, podemos formar com os dígitos: 0,1,2,3,4,5,6,7,8,9.

Auxílio: Os números iniciados por 0 não terão 2 dígitos e sua quantidade corresponde a A(9,1).

Resposta: N2=A(10,2)-A(9,1)=10×9-9=90-9=81

65.  Quantos números distintos com 3 algarismos diferentes, podemos formar com os dígitos: 0,1,2,3,4,5,6,7,8 e 9.

Auxílio: Os números iniciados por 0 não terão 3 dígitos e sua quantidade corresponde a A(9,2).

Resposta: N3=A(10,3)-A(9,2)=720-720=648

66.  Quantos números distintos com 4 algarismos diferentes, podemos formar com: 0,1,2,3,4,5,6,7,8 e 9.

Auxílio: Os números iniciados por 0 não terão 3 dígitos e sua quantidade corresponde a A(9,3).

Resposta: N4=A(10,4)-A(9,3)=5040-504=4536

67. Quantos números distintos menores que 10000 podem ser formados com algarismos diferentes da coleção: {0,1,2,3,4,5,6,7,8,9}.

Resposta: N=N1+N2+N3+N4=9+81+648+4536=5274

68.  No sistema decimal de numeração, quantos números existem com 4 algarismos com 2 algarismos repetidos?

Auxílio: A quantidade de números distintos com 4 algarismos é 4536 e a quantidade total de números (com repetição ou não) com 4 algarismos é 9000.

Resposta: N=9000-4536=4464

69.  Com as 5 vogais: A,E,I,O,U, obter o conjunto solução que contém todos os arranjos tomados 2 a 2.

70. Usando-se apenas os algarismos 1,3,5,7,9 quantos números com 3 algarismos podem ser montados?

Auxílio: A=A(m,p)=m!/(m-p)!, m=5, p=3

Resposta: A=5!/2!=60

71.  Usando-se os algarismos 0,1,2,3,4,5,6,7,8,9 quantos números com 4 algarismos podem ser montados?

Auxílio: A=A(m,p)=m!/(m-p)!, m=10, p=4

Resposta: A=10!/6!=5040

72.  Usando-se as 26 letras do alfabeto: A,B,C,D,...,Z quantos arranjos distintos com 3 letras podem ser montados?

Auxílio: A=A(m,p)=m!/(m-p)!, m=26, p=3

Resposta: A=26!/23!=26.25.24=15600

73.  Com as 26 letras do alfabeto: A,B,C,D,...,Z e os algarismos 0,1,2,3,4,5,6,7,8,9, quantas placas de carros podem ser escritas contendo 3 letras seguidas de 4 algarismos?

Auxílio: A=A(m,p)=m!/(m-p)!, m=26, p=3, n=10, q=4

Resposta: A=(26!/23!).(10!/6!)=78624000

74.  Consideremos um baralho contendo 52 cartas distintas.

a.     Quantos pares distintos podem ser formados?

b.    Quantas trincas distintas podem ser formados?

c.     Quantas quadras distintas podem ser formados?

d.    Quantos pares distintos podem ser formados tendo pelo menos um "Ás"?

e.     Quantos pares distintas podem ser formados tendo pelo menos um "Ás" e um "Rei"?

f.     Quantas trincas distintas podem ser formados tendo pelo menos um "Ás"?

g.    Quantas trincas distintas podem ser formados tendo pelo menos um "Ás" e um "Rei"?

Exercícios de arranjos com repetição

75.  Quantos números com 4 algarismos podemos formar com os algarismos: 0,1,2,3,4,5,6,7,8 e 9.

Resposta: Ar(10,4)=104=10000

76.  Quantas palavras com 3 letras podemos formar com as 26 letras de nosso alfabeto?

Resposta: Ar(26,3)=263=17576

77.  Quantas placas são possíveis em nosso sistema de trânsito, se em todas devem aparecer 3 letras seguidas por 4 números?

Resposta: N=Ar(26,3).Ar(10,4)=175760000

78.  No sistema decimal de numeração, quantos números existem com 1 algarismo?

Resposta: N1=Ar(10,1)-Ar(10,0)=10-1=9

79. No sistema decimal de numeração, quantos números existem com 2 algarismos (repetidos ou não)?

Auxílio: São 10=Ar(10,1) os números com 2 dígitos iniciados por 0.

Resposta: N2=Ar(10,2)-Ar(10,1)=102-101=100-10=90

80.  No sistema decimal de numeração, quantos números existem com 3 algarismos (repetidos ou não)?

Auxílio: Existem 100=Ar(10,2) números com 3 dígitos iniciados por 0.

Resposta: N3=Ar(10,3)- Ar(10,2)=103-102=900

81.  No sistema decimal de numeração, quantos números existem com 4 algarismos (repetidos ou não)?

Auxílio: São 100=Ar(10,3) os números com 4 dígitos iniciados por 0.

Resposta: N4=Ar(10,4)-Ar(10,3)=104-103=9000

82.  No sistema decimal de numeração, quantos números existem com n algarismos (repetidos ou não)?

Auxílio: São Ar(10,n-1) os números com n-1 dígitos iniciados por 0.

Resposta: N4=Ar(10,n)-Ar(10,n-1)=10n-10n-1=9×10n-1

83.  Num sistema de numeração com a base tendo b algarismos, quantos números existem com n algarismos (repetidos ou não)?

Auxílio: São Ar(b,n-1) os números com n-1 dígitos iniciados por 0.

Resposta: N4=Ar(b,n)-Ar(b,n-1)=bn-bn-1=(b-1)×bn-1

84.  No sistema decimal de numeração, existem quantos números pares com 4 algarismos (repetidos ou não)?

85. No sistema decimal de numeração, existem quantos números ímpares com 4 algarismos (repetidos ou não)?

86. No sistema decimal de numeração, existem quantos números pares diferentes com 4 algarismos?

87.  No sistema decimal de numeração, existem quantos números ímpares diferentes com 4 algarismos?

Resposta: N=5.A(8,3)=1.680

88.  No sistema decimal de numeração, existem quantos números pares com 4 algarismos (repetidos ou não)?

89.  No sistema decimal de numeração, existem quantos números pares com 4 algarismos (repetidos ou não)?

90.  Quantos números menores do que 10.000, podem ser formados com os algarismos 1,2,3 e 4?

Auxílio: N=Ar(4,1)+Ar(4,2)+Ar(4,3)+Ar(4,4)

Resposta: N= 41+42+43+44= 4+16+64+256=340

91.  Quantos números de 3 dígitos podem ser formados com 5 algarismos?

Auxílio:Fórmula Ar(m,p)=mp, m=5, p=3

Resposta: Ar=53=125

Exercícios de arranjos condicionais

92.  Quantos arranjos dos elementos A,B,C,D,E,F,G tomados 4 a 4, começam com duas letras dentre A,B e C?

Auxílio: N=A(m1,p1).A(m-m1,p-p1)

m=7, p=4, m1=3, p1=2

Resposta: N=A(3,2).A(4,2)=3!/1! . 4!/2!=72

93.  Com os algarismos 0,1,2,3,4,5,6,7,8,9, tomados 6 a 6, quantos números podem ser formados tendo nas duas posições iniciais algarismos que são números ímpares?

Auxílio: N=A(m1,p1).A(m-m1,p-p1), m=10, p=6, m1=5, p1=2

Resposta: N=A(5,2).A(5,4)=5!/3! . 5!/1!=2400

94.  Dentre os arranjos de 5 letras: A,B,C,D,E, tomados 3 a 3, quantos contêm a letra E?

Auxílio: N=(p-p1+1).A(m1,p1).A(m-m1,p-p1), m=5, p=3, m1=1, p1=1

Resposta: N=(3-1+1).A(1,1).A(4,2)=36

95.  Dentre os arranjos de 5 letras: A,B,C,D,E, tomados 3 a 3, quantos contêm juntas as duas letras A e B?

Auxílio: N=(p-p1+1).A(m1,p1).A(m-m1,p-p1), m=5, p=3, m1=2, p1=2

Resposta: N=(4-2+1).A(2,2).A(3,1)=18

96.  Dentre os arranjos de 6 letras: A,B,C,D,E,F, tomados 4 a 4, quantos contêm a letra A?

Auxílio: N=(p-p1+1).A(m1,p1).A(m-m1,p-p1), m=6, p=4, m1=1, p1=1

Resposta: N=(4-1+1).A(1,1).A(5,3)=240

97.  Dentre os arranjos de 6 letras: A,B,C,D,E,F, tomados 4 a 4, quantos contêm juntas 2 das 3 letras A,B e C?

Auxílio: N=(p-p1+1).A(m1,p1).A(m-m1,p-p1), m=6, p=4, m1=3, p1=2

Resposta: N=(4-2+1).A(3,2).A(3,2)=108

98.  Dentre os arranjos de 4 letras: A,B,C,D, tomados 3 a 3, quantos contêm a letra A?

Auxílio: N=(p-p1+1).A(m1,p1).A(m-m1,p-p1), m=4, p=3, m1=1, p1=1

Resposta: N=(3-1+1).A(1,1).A(3,2)=18

99.  Dentre os arranjos de 4 letras: A,B,C e D, tomados 3 a 3, quantos começam pelas letras A e B?

Auxílio: N=A(m1,p1).A(m-m1,p-p1), m=4, p=3, m1=2, p1=2

Resposta: N=A(2,2).A(2,1)=4

100.  Dentre os arranjos de 4 letras: A,B,C e D, tomados 3 a 3, quantos contêm juntos as letras A e B?

Auxílio: N=(p-p1+1).A(m1,p1).A(m-m1,p-p1), m=4, p=3, m1=2, p1=2

Resposta: N=(3-2+1).A(2,2).A(2,1)=8

Exercícios com o fatorial

101.  Se C(n,2)=28, qual é o valor de n?

Resposta: n=8.

102.  Existe um número n natural tal que C(n,3)=C(n,2)?

103.  Usando o desenvolvimento binomial de (1+1)n, demonstrar que:

C(n,0)+C(n,1)+C(n,2)+...+C(n,n)=2n

104.  Usar o PIF (Princípio de Indução Matemática), para demonstrar que:

(p+1)·C(n,p+1)=(n-p)·C(n,p).

105.  Usar o PIF (Princípio de Indução Matemática), para demonstrar que:

n·C(n-1,p)=(n-p)·C(n,p).

106.  Se A(n,2)=42, qual é o valor de n?

Resposta: n=7.

107.   Justificar a afirmação: "Se n é um número primo e p<n, então n é um divisor de C(n,p)."

108.  Usar o PIF (Princípio de Indução Matemática), para demonstrar que:

2·4·6·8·10·...2n=(2n)n!

109.   Usar o PIF (Princípio de Indução Matemática), para demonstrar que:

1·3·5·7·9· ... (2n-1)=(2n)!/[2n·n!]

Exercícios com a regra do produto

117.   Numa festa, três meninos devem ser apresentados a 5 meninas. De quantas maneiras possíveis eles podem ser apresentados?

Auxílio: N=p×q, p=3, q=5

Resposta: N=3×5=15

118.   Existem quatro estradas ligando duas cidades A e B, e três estradas ligando as cidades B e C. De quantos modos diferentes uma pessoa pode se deslocar da cidade A até a cidade C?

Auxílio: N=p×q, p=4, q=3

Resposta: N=4×3=12

119.   Uma sala possui 3 portas. Quantas possibilidades existem para que uma pessoa possa entrar e sair desta sala?

Auxílio: N=p×q, p=3, q=3

Resposta: N=3×3=9

Mais exercícios do Princípio fundamental da contagem ou Princípio multiplicativo

1) - Quantas placas (distintas) de automóveis, poderão ser emitidas; com o sistema atual de emplacamento?

2) Obtenha o total de linhas telefônicas que podem ser instaladas, com o prefixo 436, se os telefones têm 7 algarismos (ex 436-0000).

3) Quantos números ímpares de 3 algarismos distintos, são possíveis utilizando os algarismos: 1, 3, 4, 5, 7, 8. ?

4) Uma garota tem 3 saias e 4 blusas. De quantas maneiras ela poderá sair usando saia e blusa sem repetir o mesmo conjunto?

5 ) Um rapaz dispõe de 6 calças, 9 camisas e 2 pares de sapatos. Com estas peças, quantos conjuntos diferentes de calça, camisa e sapato ele pode formar para vestir-se?

6) Para a diretoria de uma firma concorrem 4 candidatos a presidente e 2 a vice-presidente. Quantas chapas podem ser formadas?

7) Um salão possui 10 portas. Pergunta-se:

a) quantas são as possibilidades de uma pessoa entrar no salão e sair dele?

b) quantas são as possibilidades de uma pessoa entrar por uma porta e sair por outra diferente?

8) Uma bandeira deve ser formada por três faixas de cores diferentes escolhidas entre 10 cores diferentes.

De quantas maneiras essa bandeira pode ser composta?

9) Quantos números de 3 algarismos podemos formar com os algarismos 1, 2, 4, 8 e 9?

10) Quantos números de 4 algarismos distintos podemos formar com os algarismos 3, 5, 6, 7 e 8?

11) Dados os algarismos 1,3, 4, 7 e 8, pergunta-se:

a) quantos números de 3 algarismos podemos formar?

b) quantos números de 3 algarismos, iniciando por 8, podemos formar?

c) quantos números de 3 algarismos, não iniciando por 4, podemos formar?

d) quantos números de 3 algarismos distintos terminam por 3?

12) Numa cidade os números de telefone tem 6 algarismos. Determine:

a) o número de telefones que podem ser formados, sabendo-se que os números não podem começar por zero;

b) quantos telefones existem com prefixos 47;

c) quantos telefones terminam por 3.

13) (FGV/2005) Em uma gaveta de armário de um quarto escuro há 6 camisetas vermelhas, 10 camisetas brancas e 7 camisetas pretas. Qual é o número mínimo de camisetas que se deve retirar da gaveta, sem que se vejam suas cores, para que:

a) Se tenha certeza de ter retirado duas camisetas de cores diferentes.

b) Se tenha certeza de ter retirado duas camisetas de mesma cor.

c) Se tenha certeza de ter retirado pelo menos uma camiseta de cada cor.

14) (Enem/2004)No Nordeste brasileiro, é comum encontrarmos peças de artesanato constituídas por garrafas preenchidas com areia de diferentes cores, formando desenhos. Um artesão deseja fazer peças com areia de cores cinza, azul, verde e amarela, mantendo o mesmo desenho, mas variando as cores da paisagem (casa, palmeira e fundo), conforme a figura.

O fundo pode ser representado nas cores azul ou cinza; a casa, nas cores azul, verde ou amarela; e a palmeira, nas cores cinza ou verde. Se o fundo não pode ter a mesma cor nem da casa nem da palmeira, por uma questão de contraste, então o número de variações que podem ser obtidas para a paisagem é

a)    6. b) 7. c) 8. d) 9. e) 10.

15) (UFES/2002) Num aparelho telefônico, as dez teclas numeradas estão dispostas em fileiras horizontais, conforme indica a figura a seguir. Seja N a quantidade de números de telefone com 8 dígitos, que começam pelo dígito 3 e terminam pelo dígito zero, e, além disso, o 2o e o 3o dígitos são da primeira fileira do teclado, o 4o e o 5o dígitos são da segunda fileira, e o 6o e o 7o são da terceira fileira.

O valor de N é

a)    27 b) 216 c) 512 d) 729 e) 1.331

16) (UFC/2002) A quantidade de números inteiros, positivos e ímpares, formados por três algarismos distintos, escolhidos dentre os algarismos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9, é igual a:

a) 320 b) 332 c) 348 d) 360 e) 384

17)(UFAL/200) Quantos números pares de quatro algarismos distintos podem ser formados com os elementos do conjunto A={0,1,2,3,4}?

a) 60 b) 48 c) 36 d) 24 e) 18

18)(UFPI/2000) Escrevendo-se em ordem decrescente todos os números de cinco algarismos distintos formados pelos algarismos 3, 5, 7, 8 e 9, a ordem do número 75389 é:

a) 54 b) 67 c) 66 d) 55 e) 56

19)(UFAL/99) Com os elementos do conjunto {1, 2, 3, 4, 5, 6, 7} formam-se números de 4 algarismos distintos. Quantos dos números formados NÃO são divisíveis por 5?

a) 15 b) 120 c) 343 d) 720 e) 840

20)(ITA/2001) Considere os números de 2 a 6 algarismos distintos formados utilizando-se apenas 1, 2, 4, 5, 7 e 8. Quantos destes números são ímpares e começam com um dígito par?

a) 375 b) 465 c) 545 d) 585 e) 625

21)(UNESP/2000) Um turista, em viagem de férias pela Europa, observou pelo mapa que, para ir da cidade A à cidade B, havia três rodovias e duas ferrovias e que, para ir de B até uma outra cidade, C, havia duas rodovias e duas ferrovias. O número de percursos diferentes que o turista pode fazer para ir de A até C, passando pela cidade B e utilizando rodovia e trem obrigatoriamente, mas em qualquer ordem, é:

a) 9. b) 10. c) 12. d) 15. e) 20.

22)(UECE/99) Quantos números ímpares, cada um com três algarismos, podem ser formados com os algarismos 2,3,4,6 e 7, se a repetição de algarismos é permitida?

a) 60 b) 50 c) 40 d) 30

GABARITO:

Respostas

1) 175760000 2) 10000 3) 80 4) 12 5)108 6) 8 7a) 100 7b) 90 8) 720 9)125

10) 120 11a) 125 11b) 25 11c)100 11d) 12 12a) 900000 12b)10000 12c) 100000

13) a)11 b)4 c)18 14)B 15)D 16)A 17)A 18)C 19)D 20)D 21)B 22)B